In our previous blog, ‘Noisy quantum computing: overcoming quantum decoherence’, we discussed how the extreme sensitivity of quantum processors continues to inhibit the realisation of large-scale quantum computing. In particular, without sufficient means of ‘quantum error correction ’ to protect delicate quantum states from environmental noise, all but the most simple of quantum computations remain susceptible to fatal errors. This is the era of ‘Noisy Intermediate Scale Quantum (NISQ)’ technology, characterised by limited error correction and confinement in scale to a hundred or so qubits.
Quantum-classical hybrid systems
While there is no shortage of proposed solutions to the issue of quantum error correction (see, for example, topological quantum computing), these all correspond to longer-term projects and, realistically, we can expect to wait many years, perhaps decades, for a true ‘quantum revolution’. This is not to say, however, that the primitive NISQ machines available today are unable to have a meaningful impact in the shorter term; notably, many researchers have turned to hybrid systems in which classical computers are augmented with quantum hardware. Such systems are designed to compensate for the limited computational capacity of present-day quantum computers by offloading large chunks of processing to a classical computer. The lure, therefore, of hybrid systems lies in their ability to utilise NISQ technology despite its limitations.
Perhaps the most promising application for this technology lies within the field of computational quantum chemistry (itself often linked to advances in drug discovery and materials science). Indeed, it is within this field that we come across the flagship example of the quantum-classical hybrid approach: the Variational Quantum Eigensolver (VQE) - an algorithmic method commonly used to estimate the ground state energy of a molecule, that is, the energy of the most stable state of a molecule. It should be noted that the ground state energy is an especially important value from which a variety of useful molecular properties can be derived. However, it is notoriously difficult (often impossible) to calculate with exact ‘analytical’ precision due to the complex arrangement of electrons within molecules. It’s for this reason that we turn to methods of approximation such as VQE.
Variational Quantum Eigensolver
Based on the ‘variational principle’ of quantum mechanics, VQE is an iterative process that takes as input an assumption about the mathematical description, or ‘wavefunction’, of a complex quantum system (such as a molecule) and generates a sequence of increasingly accurate values for the energy levels of the system.
…but how does VQE work in practice? More specifically, how does a quantum-classical hybrid system use VQE to calculate molecular ground state energy? Let’s break it down.
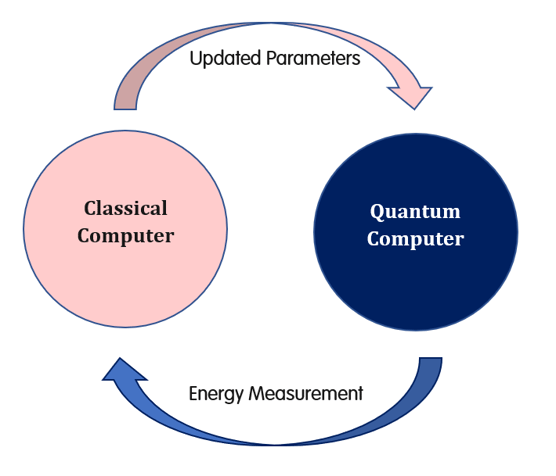
Quantum Steps: First, an educated guess is made for the electron configuration of the molecule in question, and this guess, or ‘trial configuration’, will be used as the starting point for the iterative process. As the configuration of electrons within a molecule is an inherently quantum phenomenon, a quantum computer is the perfect candidate for encoding this information. Accordingly, a quantum state representing the trial configuration is prepared by a quantum computer using what’s known as a ‘parametrised quantum circuit’, i.e., a qubit circuit with ‘tweakable’ components, with each ‘tweak’ corresponding to a (parameter) value determined by the trial configuration. In other words, the educated guess that is made for the electron configuration amounts to selecting values for each of the ‘tweakable’ components within the quantum circuit. We can think of this as modifying the quantum circuit such that it mimics the behaviour of electrons within our chosen configuration. Once the quantum state has been prepared, measurements are performed to determine the energy of the trial configuration.
Classical Steps: Next, the parameter values and energy measurement for the trial configuration are sent to a classical computer. Based on this information, the classical computer uses classical ‘optimisation’ techniques to generate a new trial configuration corresponding to a lower energy state - that is to say, the classical computer selects new values for each of the ‘tweakable’ components of the quantum circuit. This new trial configuration is then fed back to the quantum computer and used to repeat the ‘quantum steps’ described above (i.e., prepare a new quantum state and measure its energy).
Iteration: The above steps are performed repeatedly, with the classical and quantum computers operating in a feedback loop to produce a sequence of decreasing energy measurements. As each step of the iteration generates a configuration of a lower energy state, the measurements eventually converge to the energy of the lowest possible energy state, i.e., the ground state energy!*
*For completeness, note that direct convergence towards the ground state energy would in fact correspond to a best-case scenario, in which the initial guess (trial configuration) made for the electron configuration is ‘good enough’ to lead the iterative process directly towards the lowest energy configuration of all possible configurations. In reality, the initial guess may merely lead the iterative process towards the lowest energy configuration that exists within a vicinity of the trial configuration. This can be thought of as navigating a terrain of many hills and valleys in search of the deepest point (the ground state energy) - it’s usually the case that you’ll fall into several ‘false’ minima at the bottom of a shallow valley, requiring you to climb out of the valley and select a new path in order to find the ‘true’ valley floor (i.e. select a new trial configuration from which to initiate the iterative process).
Why hybrid?
Having discussed VQE in some detail, it’s useful to take a step back and remind ourselves why hybrid methods lend themselves so well to NISQ technology. As alluded to previously, lengthy computational processes cannot be sustained by present-day quantum computers because they would quickly succumb to destructive noise. The goal, therefore, is to break down such lengthy processes into a sequence of much shorter (and sustainable) processes. In the case of VQE, this is achieved by performing the (computationally intensive) optimisation steps on a classical computer, while allocating state preparation and measurement to a quantum computer - as each iteration requires only a short burst of quantum processing, this approach is ideal for the ‘noisy’ and small-scale quantum computers of the NISQ-era. This also reflects the core philosophy of quantum-classical hybrid systems: to use a quantum component for tasks that are difficult to achieve classically, and to use a classical component for tasks that are difficult (at least for now) to achieve ‘quantumly’.
Prospects
At their core, hybrid methods such as VQE are designed to solve optimisation problems, i.e., problems that involve selecting the ‘best’ solution from a large set of possible solutions. The ambiguity of the term ‘best’ reflects the broad range of problems that can be formulated in this way, and therefore the broad range of fields to which hybrid methods are applicable. In the case of VQE, the ‘best’ solution corresponds to the electron configuration that produces the lowest molecular energy; however, the ‘best’ solution could equally correspond to, e.g., an investment portfolio that produces the most profit. We can therefore expect to see NISQ-fuelled developments not only within quantum chemistry, but within a variety of other fields also amenable to optimisation techniques, such as finance and logistics.
Of course, classical computers (on their own) have been solving optimisation problems for many years (including estimations for molecular ground state energy) and will continue to do so in the future. However, there is a limit to the complexity of problems that a classical computer can handle; this is because the computational power required to solve a problem classically often scales exponentially with the difficulty of the problem (e.g. the size of a molecule to be simulated), meaning that some problems become practically impossible to solve in this way. The hope is that as we progress through the NISQ era, we will eventually produce hybrid-systems in which the quantum component (despite its lack of error correction) is sophisticated enough to produce a ‘quantum advantage’ when compared to a classical computer running alone; some experts predict that this will become a possibility within the next 2-5 years.
Nevertheless, there is a limit to the usefulness of this technology. In particular, it’s worth noting that hybrid systems are significantly constrained by the fact that their algorithms produce approximate results. This excludes immediate developments in fields such as quantum-cryptography, in which algorithms (such as ‘Shor’s Algorithm’) often rely upon exact computations and, therefore, would require a fully error corrected quantum computer to implement successfully.
Beyond the NISQ-era
While there are no well-defined standards for the technology that would ultimately bring an end to the NISQ era, it is widely believed that an error-corrected system with 10,000 to several million qubits would be necessary to achieve ‘general-purpose’ quantum computing. This is the kind of technology that we can expect to truly revolutionise the technological landscape, with far-reaching implications for our society as a whole. We’re not there yet, but there’s certainly no lack of ambition; in fact, we may see the release of a 1000 qubit system as early as 2023.
This blog was written by Michali Demetroudi.
